Capítulo 8 Medidas de curtosis o apuntamiento

En estadística, usamos la medida de curtosis para describir la “cola” de la distribución, ya que describe la forma de la misma. También es una medida del “pico” de la distribución.

wwwwwwwwwwwwwwww

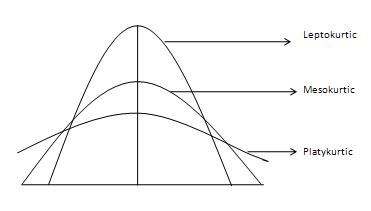
1. Mesocurtica : esta es la distribución normal
2. Leptocurtica : esta distribución tiene colas más gruesas y un pico más afilado. La curtosis es “positiva” con un valor superior a 3
3. Platicurtica : La distribución tiene un pico más bajo y más ancho y colas más delgadas. La curtosis es “negativa” con un valor superior a 30.263

• En base a la media y desviación típica

\[k= \frac{\sum_{i=1}^{n}\left( x_i-\overline{x}\right)^4 }{ns^4};\] Si \(k=3\) además \(k\geq 3\)

• En base a percentiles \[k= \frac{P_{75}-P_{25}}{2\left( P_{90}-P_{10} \right) }\] Si \(k<3\) y si \(k=3\) ademas \(k\geq 0.263\)

Si este coeficiente es nulo, la distribución se dice normal (similar a la distribución normal de Gauss) y recibe el nombre de mesocúrtica.

Si el coeficiente es positivo, la distribución se llama leptocúrtica, más puntiaguda que la anterior. Hay una mayor concentración de los datos en torno a la media.

Si el coeficiente es negativo, la distribución se llama platicúrtica y hay una menor concentración de datos en torno a la media. sería más achatada que la primera.