B Matrices
Una matriz es un arreglo de números distribuidos en filas y columnas por ejemplo la siguiente matriz \[A=\begin{pmatrix} a_{11}&a_{12}&\ldots&a_{1n}\\ a_{21}&a_{22}&\ldots&a_{2n}\\ \vdots & \vdots & \ddots &\vdots \\ a_{11}&a_{11}&\ldots&a_{nm} \end{pmatrix}_{n\times m}\] de orden \(n\times m\) tiene entradas \(a_{ij}\) donde el primer subindice indica la fila y el segundo la columna; es usual representar por simplicidad una matriz por \(A=[a_{ij}]_{n\times m}\). Si en el orden \(n=m\) entonces la matriz recibe el nombre de matriz cuadrada la suma de los elementos de la diagonal de una matriz cuadrada \(\sum_{i=1}^na_{ii}\) se llama traza. Si todas las \(a_{ij}\) son cero entonces la matriz \(A=0\) recibe el nombre matriz nula.
Dos matrices son iguales si tienen el mismo orden y cada una de las entradas respectivas son iguales es decir \(A=[a_{ij}]_{n\times m}\) y \(B=[b_{ij}]_{n\times m}\) son iguales si \(a_{ij}=b_{ij}\), \(i=1,2,\ldots n\) y \(j=1,2,\ldots m\)
B.1 Algebra de matrices
Sean las matrices \[A=[a_{ij}]_{n\times m}=\begin{pmatrix} a_{11}&a_{12}&\ldots&a_{1n}\\ a_{21}&a_{22}&\ldots&a_{2n}\\ \vdots & \vdots & \ddots &\vdots \\ a_{11}&a_{11}&\ldots&a_{nm} \end{pmatrix}_{n\times m}\] y \[B=[b_{ij}]_{p\times q}=\begin{pmatrix} b_{11}&b_{12}&\ldots&b_{1n}\\ b_{21}&b_{22}&\ldots&b_{2n}\\ \vdots & \vdots & \ddots &\vdots \\ b_{11}&b_{11}&\ldots&b_{pq} \end{pmatrix}_{p\times q}\] entonces la suma y producto de matrices se definen
Sea \(k\) un escalar entonces se verifica que \(kA=[ka_{ij}]\), \(i=1,2,\ldots n\) y \(j=1,2,\ldots m\) es decir el escalar \(k\) multiplica a cada una de las entradas de la matriz. \[\begin{align*} kA&=k[a_{ij}]_{n\times m}\\ &=[ka_{ij}]_{n\times m}\\ &=\begin{pmatrix} ka_{11}&ka_{12}&\ldots&ka_{1n}\\ ka_{21}&ka_{22}&\ldots&ka_{2n}\\ \vdots & \vdots & \ddots &\vdots \\ ka_{11}&ka_{11}&\ldots&ka_{nm} \end{pmatrix}_{n\times m} \end{align*}\]
La suma o diferencia es posible si \(n=p\) y \(m=q\) es decir los ordenes de \(A\) y \(B\) son iguales, entonces la suma o diferencia resulta \[\begin{align*} A\pm B&=[a_{ij}+b_{ij}]_{n\times m}\\ &=\begin{pmatrix} a_{11} + b_{11}&a_{12} + b_{12}&\ldots&a_{1n} + b_{1n}\\ a_{21} + b_{21}&a_{22} + b_{22}&\ldots&a_{2n} + b_{2n}\\ \vdots & \vdots & \ddots &\vdots \\ a_{11} + b_{11}&a_{11} + b_{11}&\ldots&a_{nm} + b_{nm} \end{pmatrix}_{n\times m} \end{align*}\] donde \(i=1,2,\ldots n\) y \(j=1,2,\ldots m\)
El producto es posible si \(m=p\) es decir el número columnas de la primera matriz es igual al número de filas de la segunda matriz, el orden de la matriz resultante es \(n\times q\) además \[\begin{align*} A\cdot B&=\left[\sum_{k=1}^pa_{ik}b_{kj}\right]_{n\times q}\\ &=\begin{pmatrix} \sum_{k=1}^ma_{1k}b_{k1}&\sum_{k=1}^ma_{1k}b_{k2}&\ldots&\sum_{k=1}^ma_{1k}b_{kq}\\ \sum_{k=1}^ma_{2k}b_{k1}&\sum_{k=1}^ma_{2k}b_{k2}&\ldots&\sum_{k=1}^ma_{2k}b_{kq}\\ \vdots & \vdots & \ddots &\vdots \\ \sum_{k=1}^ma_{nk}b_{k1}&\sum_{k=1}^ma_{nk}b_{k2}&\ldots&\sum_{k=1}^ma_{nk}b_{kq}\\ \end{pmatrix}_{n\times q} \end{align*}\]
donde \(i=1,2,\ldots n\) y \(j=1,2,\ldots m\)
Ejemplo B.1 Sean \(\begin{pmatrix} 3&-1&2\\ 2&-1&2\\ 1&-1&0\\ 5&0&0\\ \end{pmatrix}_{4\times 3}\) y \(\begin{pmatrix} 0&-1&2&2&0\\ 1&-1&-2&1&1\\ 3&-1&-3&5&2\\ \end{pmatrix}_{3\times 5}\) entonces \(A\cdot B=\begin{pmatrix} 5&-4&2&15&3\\ 5&-3&0&13&3\\ -1&0&4&1&-1\\ 0&-5&10&10&0\\ \end{pmatrix}_{4\times 5}\)
En caso de ser posible la multiplicación entre \(A\), \(B\) y \(C\) entonces se verfican las siguientes propiedades
- \(A(B+C)=AB+AC\)
- \((A+B)C\)
- \(A(BC)=(AB)C\)
B.2 Matrices particulares
En esta seccion se considera las siguientes matrices: Matriz triangular, matriz particular de una matriz cuadrada, matriz transpuesta, matriz simetrica, matriz conjugada, matriz hermitica, matriz escalonada.
B.2.1 Matriz triangular
Una matriz cuadrada \(A\) cuyos elementos \(a_{ij}=0\) si \(i>j\) es decir \[A=\begin{pmatrix} a_{11}&a_{12}&\ldots&a_{1n}\\ 0&a_{22}&\ldots&a_{2n}\\ \vdots & \vdots & \ddots &\vdots \\ 0&0&\ldots&a_{nn} \end{pmatrix}_{n\times n}\] se llama matriz triangular superior; reciprocamente si \(i<j\) es decir \[A=\begin{pmatrix} a_{11}&0&\ldots&0\\ a_{21}&a_{22}&\ldots&0\\ \vdots & \vdots & \ddots &\vdots \\ a_{11}&a_{11}&\ldots&a_{nn} \end{pmatrix}_{n\times n}\] se llama matriz triangular inferior. Si \(A\) es a la vez matriz triangular superior y matriz triangular inferior entonces recibe el nombre de matriz diagonal, representada por \[ \left(a_{11}, a_{22}, \ldots, a_{nn}\right) \] además si \(a_{11}= a_{22}= \ldots = a_{nn}=k\) la matriz recibe el nombre de matriz escalar y si \(k=1\) la matriz recibe el nombre de matriz unidad representada por \(I_n\) por ejemplo \[I_3=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \]
B.2.2 Matriz particular de una matriz cuadrada
B.2.3 Matriz transpuesta
B.2.4 Matriz simetrica
B.2.5 Matriz conjugada
B.2.6 Matriz hermitica
B.2.7 Matriz escalonada
\[ \begin{pmatrix} w & warnwww & w \\ w & warnwww & w \\ \end{pmatrix}_{4\times 3} \]
xw = 'Es decir los elementos son demagogos y déspotas'
x1 = 'Es decir los elementos son demagogos y déspotas'\[ \frac{\sin x}{x^3} = 0.3794281 \]
\[ \Phi_{\mu , \sigma ^{2}}(x)=\frac {1}{\sigma {\sqrt {2\pi }}}e^{-{\frac {(u-\mu )^{2}}{2\sigma ^{2}}}}du \]
Www \[\frac{1}{20\sqrt{2\pi }}\int_{-\infty }^{ 300}e^{- \frac{1}{2}\left(\frac{z-200}{20}\right)^2}dz=0.9999997\]
0.9500042 also Es decir los elementos son demagogos y déspotas
Es decir los elementos son demagogos y déspotas
Tabla B.1
| Option | N | w | Observation | Description |
|---|---|---|---|---|
| Es decir los elementos son demagogos y déspotas Es decir los elementos son demagogos y déspotas | 1 | w | Es decir los elementos son demagogos y déspotas | Es decir los elementos son demagogos y déspotas Es decir los elementos son demagogos y déspotas |
| Engine | 2 | w | Es decir los elementos son demagogos y déspotas \(\sum^{n}_{i=1}{f_i}\) | Engine to be used for processing templates. Handlebars is the default. |
| Es decir los elementos son demagogos y déspotas | 3 | w | \(\sum^{n}_{i=1}{f_i}\) | extension to be used for dest files. |
variable aleatoria Variable aleatoria entonces
2.7182818 0.9750021 0.7881446
2561
The value of x in the Python session is Es decir los elementos son demagogos y déspotas .
It is not the same x as the one in R.
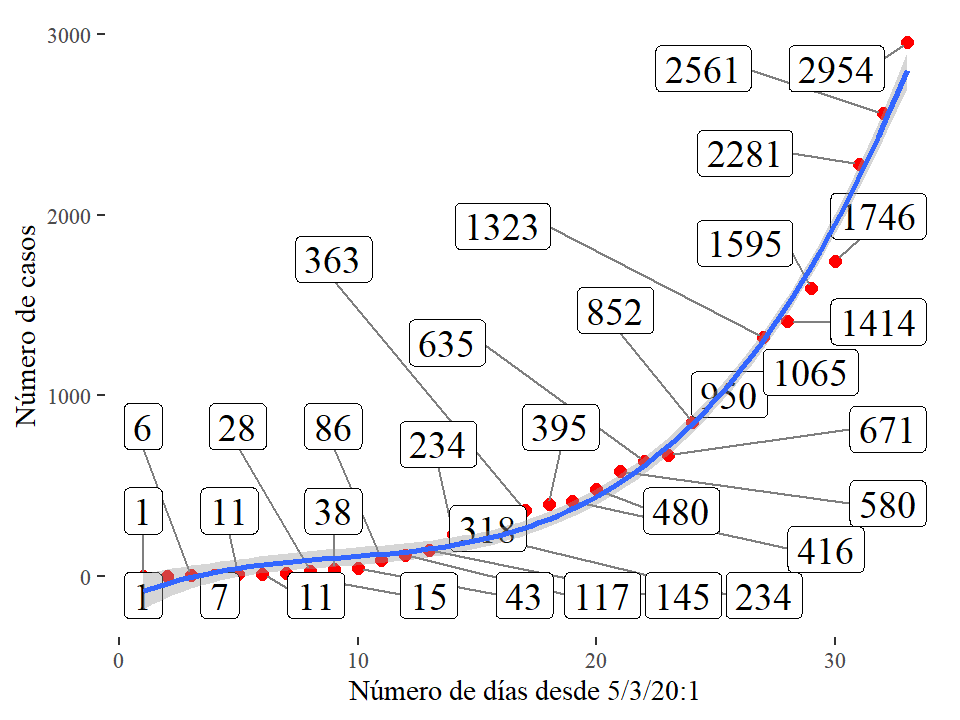
Figura B.1: Regresión lineal
## (Intercept)
## 12917.13